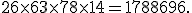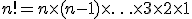Aug
30
Two numbers
Filed Under hisabati by Mucheru | Comments Off on Two numbers
Here is an interesting puzzle that was posted to one of the discussion groups at work.
A teacher tells two students that he is thinking of two natural numbers greater than 1. He tells the first student the product of the two numbers and the second one their sum. The students then have the following dialog:
First: I do not know their sum.
Second: I knew that. Their sum is less than 14.
First: I knew that, and now I know the numbers.
Second: So do I.
What were the numbers and how did they figure them out?
Solution
Let’s say that the two numbers that the teacher is thinking of are a and b. Lets say that the product a*b = n and the sum a+b = m.
When the first student gets the product n, it is fair to assume that he tries to factor n to find out the two numbers. There may be multiple ways of factoring n into two integers greater than 1 so we can assume he finds all such pairs.
When the second student gets the sum m, he tries to find all integer pairs {i,j} such that i+j = m.
Both students have their lists of candidate pairs before they start their conversation. We can now step through their statements.
First student says: ” I do not know their sum”
Remember that the first student has the product n and has determined all pairs {i,j} such that i*j=n. If he cannot find the sum, this implies that there are multiple ways of factoring n into two integers. Otherwise, if there was only one way of factoring n into two, he would have a single pair {i,j} and would be able to determine the sum.
If n cannot be factored uniquely into two numbers, then the target numbers a and b cannot both be prime (maybe one or zero of them is prime). Otherwise, if a and b were both prime, then there would only be one way of factoring n into two.
Second student says: “I knew that the first student could not know the sum”
Recall that second student has the sum m and has enumerated all pairs {i,j} such that i+j = m. Since he has these pairs, he can calculate all the possible products of i*j and this will help him know what kind of info the first student has.
When the first student says that he cannot uniquely determine the sum, it confirms what second knew. In second student’s list of pairs {i,j} , there is no pair such that, given the product, you can uniquely identify the sum.
The only way that second student could have known for sure that the first student could not determine the sum is if on the list of pairs that second student has, there is no pair {i,j} such that both i and j are prime.
In other words, m is an integer that cannot be created by adding two primes.
Second student says: The sum is less than 14
This tells us that 1 < m < 14. From the previous section , we also know that m cannot be created by adding two primes. This tells us that m = 11.
The derivation is as follows:
m is in the set {2,3,4,5,6,7,8,9,10,11,12,13}
2 is out because the only {i,j} such that i+j = 2 is {1,1} and we know that both candidate numbers are greater than 1.
3 is out because the only {i,j} s.t. i+j=3 is {1,2}
4 is out because it can be created by 2+2 where 2 is prime
5 is out. It can be created by 2+3
6 is out. It can be created by 3+3
7 is out. It can be created by 2+5
8 is out. It can be created by 3+5
9 is out. It can be created by 2+7
10 is out. It can be created by 3+7
12 is out. It can be created by 5+7
13 is out. It can be created by 2+11
First student says: “I knew that the sum m < 14”
Remember that the first student has the product n and has determined all pairs {i,j} such that i*j=n. Since he has the pairs, he has also summed them and he knows for sure that for all {i,j}, i+j <14.
In other words, n is an integer that can be factored into two in multiple ways but however you do it, the two numbers you end up with always add up to less than 14.
This is the final piece. The final derivation is as follows:
We know that i and j are both numbers in {2,3,4,5,6,7,8,9,10,11,12,13} (i.e. neither i nor j can be greater than 14)
We can enumerate all pairs {i,j} such that i+j < 14
{2|2,3,4,5,6,7,8,9,10,11}
{3|3,4,5,6,7,8,9,10}
{4|4,5,6,7,8,9}
{5|5,6,7,8}
{6|6,7}
Where the notation {x|y,z} is shorthand for the pairs “the pairs where the smaller number is x and the larger is either y or z” (i.e. {x,y} and {x,z})
We can then eliminate all pairs where i and j are both prime. This leaves.
{2|4,6,8,9,10}
{3|4,6,8,9,10}
{4|4,5,6,7,8,9}
{5|6,8}
{6|6,7}
Consider the products of pairs i*j
|
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
8 |
|
12 |
|
16 |
18 |
20 |
|
3 |
12 |
|
18 |
|
24 |
27 |
30 |
|
4 |
16 |
20 |
24 |
28 |
32 |
36 |
|
|
5 |
|
|
30 |
|
40 |
|
|
|
6 |
|
|
36 |
42 |
|
|
|
Eliminate all products that can be created by multiplying numbers that add up to >=14. This eliminates 24, 28, 30, 32, 36, 40 and 42 because :
36 = 18*2, and 18+2>14
30 = 15*2, and 15+2 > 14
24 = 12*2, and 12+2 = 14
28 = 14*2
42=21*2
32=16*2
40=20*2
This gives us the grid:
|
|
4 |
5 |
6 |
8 |
9 |
10 |
|
2 |
8 |
|
12 |
16 |
18 |
20 |
|
3 |
12 |
|
18 |
|
27 |
|
|
4 |
16 |
20 |
|
|
|
|
Which gives the pairs
{2|4,6,8,9,10}
{3|4,6,9}
{4|4,5}
We already know that i+j = 11. Looking at our pairs, we determine that the answer is {2,9}
Sep
20
Project Euler: Happy numbers
Filed Under hisabati, project euler by Mucheru | 1 Comment
Problem 92 from Project Euler asks us to find the number of non-Happy numbers under 10 million:
A number chain is created by continuously adding the square of the digits in a number to form a new number until it has been seen before.
For example,
44 -> 32 -> 13 -> 10 -> 1 -> 1
85 -> 89 -> 145 -> 42 -> 20 -> 4 -> 16 -> 37 -> 58 -> 89Therefore any chain that arrives at 1 or 89 will become stuck in an endless loop. What is most amazing is that EVERY starting number will eventually arrive at 1 or 89.
How many starting numbers below ten million will arrive at 89?
The numbers that have a sequence ending in 1 are called the ‘Happy’ numbers (making the rest non-Happy).
As with most Project Euler problems, this could be solved by brute force. Following the definition of the sequences, we can run through all numbers from 1 to 10 million. For each number, split it into its constituent digits, square each digit and sum them all. If the sum of squares of digits is 89, we’ve found a match. Otherwise, test the new number for a match (split digits, square etc). The problem with this approach is that you will have to evaluate at lest 10 million numbers. In a naive implementation, you would actually end up looking at some numbers multiple times. For example, in the series starting at 85 above, you would end up looking at 145 and you may look at it again when you consider the series starting at 145. Clearly, this approach does not scale.
The first optimization we can make is ensure we evaluate a number only once. To do this, we can store a lookup table with all the numbers that have a series ending in 89. If we evaluate a series that ends in 89, we know that any numbers in the series ends in 89 (i.e. 85,145,20 etc from above).
The second optimization comes when we notice that the largest possible sum of the squares of digits in a number for our test is (92)x7 = 567 (from the number 9999999). This reduces the number of sequence evaluations we have to make. We can construct our lookup table showing numbers between 0 and 567 that end in 89. Then for each number in our test range from 0 to 10 million, we simply calculate the sum of squares of digits and check our lookup table to see if the value would terminate in 89.
The third optimization is based on the realization that the sum of squares of digits function does not change if you reorder the digits. That is, the sum of squares for 123 is the same as for 213, 312, 321 etc. So if the sequence starting at 123 ends at 89, we know that 312, 213 etc will end at 89 as well. Formally, this means that the sum-of-squares-of-digits function partitions the set of integers into Equivalence classes such that a~b if a and b contain the same digits. Using this optimization,we only need to check sequences for 11,440 numbers – almost 1000 times smaller than the 10 million checks that the brute force approach would have us make. However, to use this approach, we need to determine the size of each equivalence class. That way, if we determine that that a particular number ends in 89, then we can update our count of matching numbers by adding the full size of the numbers equivalence class.
We turn to combinatorics to determine the size of each class. For any one number, its equivalence class is constructed by creating permutations of the digits. The size of the class is therefore given by the number of unique permutations of digits in a sequence. We need to account for repetitions of indistinguishable objects: that is, given the sequence 100335, we need to account for that the the 3s and 0s can be interchanged in permutations without resulting in different integers. The formula and reasoning for such a count is explained at http://www.andrews.edu/~calkins/math/webtexts/prod02.htm under the title “Permutations with repeated elements”. The eventual formula is;
nPr1 r2…rk = n! /( r1!r2!…rk!)
where we are arranging n elements where the first element occurs r1 times, the second r2 times …
We still need to figure out how to make sure we pick one (and only one) element from each equivalence class for our sequence calculations. Each class is composed of numbers that contain the same digits in some order. We can represent each class by creating a string with the non-decreasing sequence of digits that define the class. Generating all strings of of length 7 with non-decreasing sequence of digits will give us exactly one representative from each equivalence class.
With these optimizations, we solve the problem in 0.5 seconds using python. We can also count all the non-Happy numbers under 10^100 in under a minute. We can further reduce our computations by noticing that there are much fewer happy numbers than unhappy numbers – there are 20 happy numbers under 100. Since all numbers are either Happy or non-Happy, we can determine the number of non-Happy numbers by counting happy numbers and subtracting from the count of numbers in range.
Jan
16
Summing numbers that cannot be written as a sum of two abundant numbers
Filed Under hisabati, project euler by Mucheru | Comments Off on Summing numbers that cannot be written as a sum of two abundant numbers
Problem 23 from Project Euler asks for the sum of numbers that cannot be written as the sum of two abundant numbers:
A perfect number is a number for which the sum of its proper divisors is exactly equal to the number. For example, the sum of the proper divisors of 28 would be 1 + 2 + 4 + 7 + 14 = 28, which means that 28 is a perfect number.
A number whose proper divisors are less than the number is called deficient and a number whose proper divisors exceed the number is called abundant.
As 12 is the smallest abundant number, 1 + 2 + 3 + 4 + 6 = 16, the smallest number that can be written as the sum of two abundant numbers is 24. By mathematical analysis, it can be shown that all integers greater than 28123 can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.
Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.
When I read the problem, the requirements seemed to be pretty straight-forward. We need to find all the abundant numbers in the range so that we can determine all the numbers that are the sum of two abundant numbers. My first(naive) approach to this was terribly inefficient – it ran for hours and didn’t give the right answer. We cannot get around the need to determine the abundant numbers in range. However, we can reduce the search space when determining the numbers that are expressed as sums of two abundant numbers. To do this, we take advantage of some known properties:
- The upper bound for numbers that cannot be expressed as the sum of two numbers is actually 20161 not 28123 (as shown here).
- All even numbers greater than 48 can be written as the sum of two abundant numbers (also shown in the article here).
With these facts in mind, we are ready for the implementation. The first routine determines the abundant numbers in range.
1: def abundant_nums_in_range(n): 2: abundant=[] 3: min_abundant_not_multiple_of_2_or_3 = 5391411025 4: for i in range(1,n): 5: if(i < min_abundant_not_multiple_of_2_or_3): 6: if(i % 2 != 0) and (i%3 != 0): 7: continue 8: divisors = proper_divisors(i) 9: divisors_sum = 0 10: for d in divisors: 11: divisors_sum += d 12: if(divisors_sum > i): 13: abundant.append(i) 14: return abundant 15:
The routine that determines proper divisors of a number tests divisors from 1 to the square-root of the number and extracts all divisors in pairs.
1: def proper_divisors(n): 2: divisors =[] 3: maxValue = int(sqrt(n))+1 4: for i in range(1,maxValue): 5: if(n % i == 0): 6: if(i not in divisors): 7: divisors.append(i) 8: quotient = n/i 9: if(quotient == n): continue 10: if(quotient not in divisors): 11: divisors.append(quotient) 12: return divisors 13:
The main routine for the solution is the method that determines all numbers in range that can be expressed as sum of two numbers. Since we know that all even numbers greater than 48 are in our target set, we only need to determine odd numbers in range. The only way to get an odd number by summing two numbers is to sum an even number with an odd.
1: def abundant_pair_sums_in_range(n): 2: abundant_nums = abundant_nums_in_range(n) 3: even_abundants = [] 4: odd_abundants = [] 5: for a in abundant_nums: 6: if(a %2 == 0): 7: even_abundants.append(a) 8: else: 9: odd_abundants.append(a) 10: abundant_sum_nums = [] 11: num_even_abundants = len(even_abundants) 12: num_odd_abundants = len(odd_abundants) 13: curr_num = 0 14: abundant_nums_filter = [0 for x in range(0,n)] 15: # all even numbers >48 are the sum of two abundants 16: for a in range(0,n): 17: if(a % 2 ==0): 18: if(a > 48): 19: abundant_nums_filter[a] = 1 20: elif a in [24,30,32,36,38,40,42,44,48]: 21: abundant_nums_filter[a] = 1 22: for i in range(0, num_even_abundants): 23: for j in range(0, num_odd_abundants): 24: curr_num = even_abundants[i] + odd_abundants[j] 25: if(curr_num < n): 26: abundant_nums_filter[curr_num] = 1 27: for a in range(1,n): 28: if abundant_nums_filter[a] == 1 : 29: abundant_sum_nums.append(a) 30: return abundant_sum_nums 31:
The last routine ties all operations together.
1: def get_non_abundant_sums(n): 2: abundant_sums = abundant_pair_sums_in_range(n) 3: sum_all = sum([x for x in range(0,n)]) 4: sum_abundants = sum(abundant_sums) 5: return (sum_all - sum_abundants) 6:
Jan
2
Length of cycles in unit fractions
Filed Under hisabati, project euler by Mucheru | Leave a Comment
Problem 26 of Project Euler asks us to find the length of cycles in unit fractions:
A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:
1/2 = 0.5 1/3 = 0.(3) 1/4 = 0.25 1/5 = 0.2 1/6 = 0.1(6) 1/7 = 0.(142857) 1/8 = 0.125 1/9 = 0.(1) 1/10 = 0.1 Where 0.1(6) means 0.166666…, and has a 1-digit recurring cycle. It can be seen that 1/7 has a 6-digit recurring cycle.
Find the value of d < 1000 for which 1/d contains the longest recurring cycle in its decimal fraction part.
The decimal representations of the fractions and therefore cycles can be discovered using long division. A python implementation of this would be:
1: def unit_fraction_decimal_rep(n): 2: numerator, denominator = 1, n 3: fraction = [] 4: remainders = {} 5: while True: 6: numerator *= 10 7: r = numerator % denominator 8: q = (numerator - r)/denominator 9: if(r == 0): 10: fraction.append(q) 11: break 12: if(r in remainders.values()): 13: foundCycle = False 14: for key,value in remainders.items(): 15: if(r == value) and (q == int(fraction[key])): 16: # mark the cycle with parenthesis 17: fraction.insert(key,"(") 18: fraction.append(")") 19: foundCycle = True 20: break 21: if foundCycle: 22: break 23: remainders[len(fraction)] = r 24: fraction.append(str(q)) 25: numerator = r 26: return "0."+"".join(fraction)
To solve the problem posed, we could generate fractional representations of all integers from 1000 down and check for the longest cycles. However, looking at the algorithm above we can figure out how long a cycle will be without actually having to calculate it.
The terms in the decimal representation are determined by the remainder in each iteration of the loop starting on line 5 above. If one of the remainders is 0, then the fraction terminates. On the other hand, if we see a remainder that we have seen previously, then we have gotten to the end of a cycle. The maximum length of a cycle is n-1 since there are only n-1 possibilities for the remainder.
In each iteration of the loop on line 5, we multiply the numerator by 10. This establishes a relationship between 10 and n. We use a little algebra to explore the relationship.
- If the fraction terminates, then at some point we get a remainder of 0 meaning that n evenly divides a power of 10. Since 10 has only two divisors, 2 and 5, n evenly divides a power of 10 if and only if n = 2ax5b where a,b are non-negative integers (a or b may be 0 in which case n is either only divisible by 2 or by 5).
- The fraction will recur if n does not evenly divide any power of 10.
- If n is has no factors in common with 10 (abbreviated as n is coprime with 10), the length of the recurring cycle is equal to the order of 10 in the group Zn (the multiplicative group of integers modulo n). If 10 has order d then 10d mod n = 1 and 1 becomes the first remainder repeated (since we start with numerator 1).
- If n is not coprime with 10, there is no d for which 10d mod n = 1. In such cases n= 2ax5bxm where m is coprime with 10. So 1/n = 1/(2ax5b) x 1/m . The component 1/(2ax5b) will terminate so the cycle that results in 1/n is contributed by 1/m and the length of the cycle is equal to the order of 10 in Zm.
Applying this, we come up with the algorithm below:
1: def recurring_cycle_length(n): 2: cycleLen = 0 3: # remove powers of 2 and 5 in n 4: while (n % 2 == 0): 5: n /= 2 6: while (n % 5 == 0): 7: n /= 5 8: if n > 1: 9: a = 10 % n 10: cycleLen = 1 11: while a != 1: 12: a *= 10 13: a %= n 14: cycleLen += 1 15: return cycleLen
The longest cycle will be generated when 10 has a high order in Zn or Zm. So when searching for the longest cycle we start with the maximum value of n in the range and move down. If n is prime, the order of 10 in the Zn is either n-1 or a divisor of n-1. If we find a max value for the period which is equal to n-1, we have found the longest cycle.
1: def max_len_recurring_cycle_in_range(n): 2: # iterate from the max num down 3: maxCycleLen = 0 4: maxCycleLenGenerator = n 5: for i in range(n, 1, -1): 6: currLen = recurring_cycle_length(i) 7: if(currLen > maxCycleLen): 8: maxCycleLen = currLen 9: maxCycleLenGenerator = i 10: if(currLen == i-1): 11: break 12: return maxCycleLenGenerator, maxCycleLen
Dec
27
Project Euler: nth lexicographic permutation
Filed Under hisabati, project euler by Mucheru | Leave a Comment
Problem 24 from Project Euler asks us to find the nth lexicographic permutation of a sequence of digits:
A permutation is an ordered arrangement of objects. For example, 3124 is one possible permutation of the digits 1, 2, 3 and 4. If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of 0, 1 and 2 are:
012 021 102 120 201 210
What is the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?
My first instinct was to write a routine that would enumerate permutations of a sequence of digits in lexicographic order. This would involve two functions: the first would take a permutation and return the next lexicographic permutation of the digits. The next function would call the first 999999 times, starting with the first sequence (0123456789) and passing intermediate values as it went along. The main function is below.
1: def next_lexicographic_permutation(currPermutation): 2: digits = [int(x) for x in str(currPermutation)] 3: maxIndex = len(digits)-1 4: prevValue = digits[maxIndex] 5: currValue = digits[maxIndex] 6: for i in range(maxIndex, -1,-1): 7: currValue = digits[i] 8: if (i == 0) and (currValue == max(digits)): 9: return currPermutation 10: if(currValue < prevValue): 11: prefix = digits[:i] 12: suffix = digits[i:] 13: nextStart = min([x for x in suffix if x > currValue]) 14: suffix.remove(nextStart) 15: suffix.sort() 16: nextPermutation = "".join([str(x) for x in prefix]) +str(nextStart)+ "".join([str(x) for x in suffix]) 17: return nextPermutation 18: else: 19: prevValue = currValue 20: return currPermutation 21:
While this approach worked, the operation took 30 seconds. After looking at the problem for a while longer and consulting my muse, I realized that we could directly determine the nth permutation. It is an established fact that given a set of m elements, the number of permutations possible is given by m!( read as “m factorial”, defined here). So for our set of 10 digits, there are 10! possible permutations. Of these permutations, 1/10 of them have 0 as the first digit, 1/10 have 1 as the first etc. This comes to 9! = 362,880 permutations starting with any one digit. Since sequences are presented in lexicographic order, we know that the millionth permutation has to start with 2 ( the sequences starting with 0 end at 9! and those starting with1 end at 2*9!).
The millionth permutation of 10 digits will be the 274240th permutation from the set of permutations starting with 2 (i.e. 1000,000 – 2*9!, accounting for the permutations that started with 0 and 1). The problem of determining the 274240th permutation from the set of permutations starting with 2 is equivalent to the problem we’ve just solved for 10 digits, except that this time we are determining the 274240th permutation of the digits 013456789. To solve it,we apply the same algorithm as we did previously giving a rather neat recursive solution to the general problem.
1: def nth_lexicographic_permutation(initialPermutation, n): 2: currPermutation=str(initialPermutation) 3: if len(currPermutation) == 1: return initialPermutation 4: residue = n 5: # number of permutations starting with any one digit 6: numSuffixPermutations = factorial(len(currPermutation) - 1) 7: outputDigitIndex = 0 8: if(numSuffixPermutations < residue): 9: outputDigitIndex = residue / numSuffixPermutations 10: if(residue % numSuffixPermutations == 0): 11: outputDigitIndex -= 1 12: residue -= (outputDigitIndex * numSuffixPermutations) 13: indexDigit = currPermutation[outputDigitIndex] 14: currPermutation = currPermutation.replace(indexDigit,'') 15: return indexDigit + nth_lexicographic_permutation(currPermutation, residue) 16:
This second solution runs in less than a second!
Dec
16
Project Euler: Determining the number of paths in a grid
Filed Under hisabati, project euler by Mucheru | Comments Off on Project Euler: Determining the number of paths in a grid
For problem 15 from Project Euler, we are asked to find the number of paths leading from the top left corner of a grid to the bottom right corner that do not involve backtracking.
Starting in the top left corner of a 2 by 2 grid, there are 6 routes (without backtracking) to the bottom right corner.
How many routes are there through a 20 by 20 grid?
Given the way the problem is set up, for any one node there are at most two nodes that can lead directly to the node. If we assign coordinates to the grid with (0,0) being the top-left corner, the only nodes that have direct outgoing paths to (1,1) are (0,1) and (1,0). Trivially, each of the nodes in row 0 (the top row) has only one node that can lead into it (the node immediately to its left). Similarly, nodes in column 0 (the left-most column) each have one node leading into them (the node immediately above them). We can use this information to calculate the number of paths ending at any one node in the grid.
To do this, consider nodes A, B and C that form the lower right triangle of an arbitrary square in the grid. We label the nodes such that A is the lower left corner of the square, B is the lower right corner while C is the upper right corner of the square. As shown before, the only way to get a path ending at B is to take a path ending at either A or C and add one step to it. We also know that a path ending at A cannot pass through C (since we don’t allow backtracking) and similarly a path ending at C cannot pass through A. Therefore, the number of paths ending at B = number of paths ending at A + number of paths ending at C.
This leads to the following rather short algorithm:
1: def num_paths_to_grid_bottom(numRowCells, numColumnCells): 2: currRow = [1 for x in range(numColumnCells + 1)] 3: # the number of nodes to consider = numRowCells + 1 4: for numRow in range(1, numRowCells + 1): 5: for numColumn in range(1, numColumnCells + 1): 6: currRow[numColumn] += currRow[numColumn - 1] 7: return currRow[numColumnCells]
Nov
27
Project Euler: finding maximal sum of path in a graph
Filed Under hisabati, project euler by Mucheru | Comments Off on Project Euler: finding maximal sum of path in a graph
Problem 18 in Project Euler reminded me of shortest path algorithms in graph theory. The goal is to determine the maximal sum you can compute when traveling from the top to the bottom of a triangle.
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
3
7 5
2 4 6
8 5 9 3That is, 3 + 7 + 4 + 9 = 23.
Find the maximum total from top to bottom of the triangle below:
75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23
If this were a shortest path problem, we would be computing the minimum sum when traveling down the triangle (and we would also have a fixed destination, rather than a set of them – details, details). As phrased, the problem does not actually require us to give the path that yields the maximal sum and that eases the requirements on our algorithm.
The first step of our solution is to read lists of integers from the input triangle string.
1: def get_triangle_lists(triangleString): 2: listOfRowsString = triangleString.split('n') 3: listOfRows = [] 4: for row in listOfRowsString: 5: currRow = [int(x) for x in row.split()] 6: listOfRows.append(currRow) 7: return listOfRows
Next, we compute the max sum.
1: def max_sum_in_triangle(triangleString): 2: listOfLists = get_triangle_lists(triangleString) 3: numRows = len(listOfLists) 4: for index in range(0, numRows): 5: if(index == 0): 6: continue 7: currRow = listOfLists[index] 8: previousRow = listOfLists[index - 1] 9: for column in range(0, index+1): 10: if (column == 0): 11: currRow[column] += previousRow[column] 12: elif(column == index): 13: currRow[column] += previousRow[column - 1] 14: else: 15: currRow[column] += max(previousRow[column - 1], previousRow[column]) 16: return max(listOfLists[numRows - 1])
The motivation is simple. We go through the triangle, from top to bottom one row at a time (breadth-first). For each node, we set its value to the maximal sum that can be achieved by a valid path ending in that node. For the top node, the maximal sum is trivially the value of the node. For subsequent rows, each node can be reached from exactly one or two nodes from the previous row. The outer nodes in a row are only reachable from the outer nodes from the previous row. This means that for these nodes, we always add the current node value to the previous outer node’s value ( Lines 10 to 13 of the code above). Nodes that are not outer nodes in the row are reachable from two nodes in the previous row (the node to the upper left and one to the upper right in the graphical representation).The maximal sum at the current node is therefore given by the value of the current node plus the higher value between those presented in the two nodes in the previous row (Line 15 of the code above).
When the algorithm finishes iterating through the rows, the maximal value can be read directly from the bottom row of the triangle (line 16 in the code above).
Nov
26
Project Euler: Largest product of consecutive digits in grid
Filed Under hisabati, project euler by Mucheru | 1 Comment
Problem 11 from Project Euler is a fun one:
In the 20 by 20 grid below, four numbers along a diagonal line have been marked in red.
08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08
49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00
81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65
52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91
22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80
24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50
32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70
67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21
24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72
21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95
78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92
16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57
86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58
19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40
04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66
88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69
04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36
20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16
20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54
01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48The product of these numbers is
What is the greatest product of four adjacent numbers in any direction (up, down, left, right, or diagonally) in the 20 by 20 grid?
I came up with two solutions: a naive exhaustive search (which still runs remarkably fast in python) and a slightly more efficient one in the spirit of my solution to problem 8. The naive version proceeds as follows:
1: def max_prod_in_grid_basic(gridString, windowSize): 2: gridNums = [int(x) for x in gridString.split()] 3: gridLen = int(sqrt(len(gridNums))) 4: maxProduct = 0 5: # get horizontal products 6: lastColumn = gridLen - windowSize + 1 7: for rootRow in range(0, gridLen): 8: for rootColumn in range(0, lastColumn): 9: startIndex = (rootRow * gridLen) + rootColumn 10: endIndex = startIndex + windowSize 11: windowItems = gridNums[startIndex:endIndex] 12: currProduct = prod(windowItems) 13: if(currProduct > maxProduct): 14: maxProduct = currProduct 15: # get vertical products 16: lastRow = gridLen - windowSize + 1 17: for rootColumn in range(0, gridLen): 18: for rootRow in range(0, lastRow): 19: startIndex = (rootRow * gridLen) + rootColumn 20: endIndex = startIndex + (gridLen * windowSize) 21: windowItems = gridNums[startIndex: endIndex: gridLen] 22: currProduct = prod(windowItems) 23: if(currProduct > maxProduct): 24: maxProduct = currProduct 25: # get down-diagonal products 26: lastRow = gridLen - windowSize + 1 27: lastColumn = gridLen - windowSize + 1 28: for rootRow in range(0, lastRow): 29: for rootColumn in range(0, lastColumn): 30: startIndex = (rootRow * gridLen) + rootColumn 31: endIndex = startIndex + (gridLen * windowSize) + windowSize 32: windowItems = gridNums[startIndex: endIndex: gridLen+1] 33: currProduct = prod(windowItems) 34: if(currProduct > maxProduct): 35: maxProduct = currProduct 36: # get up-diagonal products 37: lastRow = gridLen - windowSize + 1 38: lastColumn = gridLen 39: firstColumn = windowSize - 1 40: for rootRow in range(0, lastRow): 41: for rootColumn in range(firstColumn, lastColumn): 42: startIndex = (rootRow * gridLen) + rootColumn 43: endIndex = startIndex + (gridLen * windowSize) - windowSize 44: windowItems = gridNums[startIndex: endIndex: gridLen-1] 45: currProduct = prod(windowItems) 46: if(currProduct > maxProduct): 47: maxProduct = currProduct 48: return maxProduct
The primary weakness with this approach is that it does not take advantage of the fact that there is a simple relationship between the products of two adjacent sets of consecutive numbers. From the solution to problem 8:
We achieve some performance gain by taking advantage of the overlap between adjacent windows. If the window has length 5, then adjacent windows have 3 elements in common. The overlap elements contribute the same value to the product computed for the two adjacent windows. Therefore, the difference between the product computed for a window starting at index i and one starting at i+1 is due to elements at the end of the windows. Specifically, the product of the window rooted at i+1 is given by the dividing the value of the product of the window rooted at i by the value of the ith element (undoing the effect of the element we’re removing) multiplied by the value of the element at position i+(windowSize – 1) (adding the effect of the new element)
The second algorithm takes advantage of this information. The solution is in two functions. First, we extract the list of valid sequences (all the rows, columns and up and down diagonals), taking the maximum length of each sequence.
1: def get_sequences_in_grid(gridString, minLength): 2: gridNums = [int(x) for x in gridString.split()] 3: gridLen = int(sqrt(len(gridNums))) 4: digitSequences = [] 5: # get horizontal sequences 6: rootColumn = 0 7: for rootRow in range(0, gridLen): 8: startIndex = (rootRow * gridLen) + rootColumn 9: endIndex = startIndex + gridLen 10: listItems = gridNums[startIndex:endIndex] 11: digitSequences.append(listItems) 12: # get vertical sequences 13: rootRow = 0 14: for rootColumn in range(0, gridLen): 15: startIndex = (rootRow * gridLen) + rootColumn 16: endIndex = int(len(gridNums)) 17: listItems = gridNums[startIndex: endIndex: gridLen] 18: digitSequences.append(listItems) 19: # get down-diagonal sequences 20: # upper triangle 21: lastRow = gridLen - minLength + 1 22: lastColumn = gridLen - minLength + 1 23: rootRow = 0 24: for rootColumn in range(0, lastColumn): 25: startIndex = (rootRow * gridLen) + rootColumn 26: endIndex = (rootRow + 1 +(gridLen - (rootColumn + 1))) * gridLen 27: listItems = gridNums[startIndex: endIndex: gridLen+1] 28: digitSequences.append(listItems) 29: # lower triangle 30: rootColumn = 0 31: for rootRow in range(1, lastRow): 32: startIndex = (rootRow * gridLen) + rootColumn 33: endIndex = (rootRow + 1 + (gridLen - (rootRow + 1))) * gridLen 34: listItems = gridNums[startIndex: endIndex: gridLen+1] 35: digitSequences.append(listItems) 36: # get up-diagonal sequences 37: # upper triangle 38: rootRow = 0 39: firstColumn = minLength - 1 40: for rootColumn in range(firstColumn, gridLen): 41: startIndex = (rootRow * gridLen) + rootColumn 42: endIndex = startIndex + (rootColumn * gridLen) 43: listItems = gridNums[startIndex: endIndex: gridLen - 1] 44: digitSequences.append(listItems) 45: # lower triangle 46: rootColumn = gridLen - 1 47: for rootRow in range(1, lastRow): 48: startIndex = (rootRow * gridLen) + rootColumn 49: endIndex = (rootRow + 1 + (gridLen - (rootRow + 1))) * gridLen 50: listItems = gridNums[startIndex: endIndex: gridLen - 1] 51: digitSequences.append(listItems) 52: return digitSequences 53:
The second step takes the list of sequences and iterates through them, computing the max product for each list using a modified version of the “slice product” function from problem 8.
1: def max_prod_in_grid(gridString, minLength): 2: sequences = get_sequences_in_grid(gridString, minLength) 3: max_product = 0 4: for currList in sequences: 5: listLength = len(currList) 6: if(listLength < minLength): 7: continue 8: curr_product = prod(currList[:minLength]) 9: if(curr_product > max_product): 10: max_product = curr_product 11: for i in range(1, listLength - minLength + 1): 12: stopPosition = i + (minLength - 1) 13: outItem = currList[i - 1] 14: inItem = currList[stopPosition] 15: if(outItem == 0): 16: curr_product = prod(currList[i:stopPosition + 1]) 17: else: 18: curr_product = (curr_product / outItem) * inItem 19: if(curr_product > max_product): 20: max_product = curr_product 21: return max_product
Nov
25
Project Euler: Largest product of consecutive digits
Filed Under hisabati, project euler by Mucheru | 1 Comment
For Problem 8 in Project Euler, you are required to find the largest product of 5 consecutive digits in a 1000 digit integer.
7316717653133062491922511967442657474235534919493496983520
3127745063262395783180169848018694788518438586156078911294
9495459501737958331952853208805511125406987471585238630507
1569329096329522744304355766896648950445244523161731856403
0987111217223831136222989342338030813533627661428280644448
6645238749303589072962904915604407723907138105158593079608
6670172427121883998797908792274921901699720888093776657273
3300105336788122023542180975125454059475224352584907711670
5560136048395864467063244157221553975369781797784617406495
5149290862569321978468622482839722413756570560574902614079
7296865241453510047482166370484403199890008895243450658541
2275886668811642717147992444292823086346567481391912316282
4586178664583591245665294765456828489128831426076900422421
9022671055626321111109370544217506941658960408071984038509
6245544436298123098787992724428490918884580156166097919133
8754992005240636899125607176060588611646710940507754100225
6983155200055935729725716362695618826704282524836008232575
30420752963450
My implementation for this proceeds as follows:
1: def window_slice_product(num,windowSize): 2: digits = [int(x) for x in str(num)] 3: sequencewindowSize = len(digits) 4: if(sequencewindowSize <= windowSize): 5: return prod(digits) 6: 7: products =[] 8: curr_product = prod(digits[:windowSize]) 9: max_product = curr_product 10: for i in range(1, sequencewindowSize - windowSize + 1): 11: stopPosition = i + (windowSize - 1) 12: outItem = digits[i - 1] 13: inItem = digits[stopPosition] 14: if(outItem == 0): 15: curr_product = prod(digits[i:stopPosition + 1]) 16: else: 17: curr_product = (curr_product / outItem) * inItem 18: if(curr_product > max_product): 19: max_product = curr_product 20: return max_product
Given the digits in the input number, we create a list with all the integers in sequence. To calculate the required product, we create a sliding window of length 5, which serves as a snapshot of the list. In each iteration of the loop starting on line 10, we ‘slide’ the window down the list (we start with the window’s first element at index 0 and consider 5 consecutive items; move the window to have first item at index 1 and consider 5 items etc until we get to the point where the window’s starting element is at index 995). We take the product of each window and check if it’s higher than the maximal product seen so far. At the end, we report the max product.
We achieve some performance gain by taking advantage of the overlap between adjacent windows. If the window has length 5, then adjacent windows have 3 elements in common. The overlap elements contribute the same value to the product computed for the two adjacent windows. Therefore, the difference between the product computed for a window starting at index i and one starting at i+1 is due to elements at the end of the windows. Specifically, the product of the window rooted at i+1 is given by the dividing the value of the product of the window rooted at i by the value of the ith element (undoing the effect of the element we’re removing) multiplied by the value of the element at position i+(windowSize – 1) (adding the effect of the new element). This is achieved in lines 11 to 17 of the algorithm posted.
In the cases where we remove a zero, its necessary to compute the product for the new window by multiplying all items in the window – otherwise we would end up dividing by zero.
Nov
24
Project Euler: Summing digits in a factorial
Filed Under hisabati, project euler by Mucheru | Leave a Comment
For problem 20, the goal is to sum all the digits in a large number:
Find the sum of the digits in the number 100!
The algorithm proceeds as follows:
1: def factorial(n): 2: if(n == 0): 3: return 1 4: else: 5: return (n * factorial(n-1)) 6: 7: def sum_factorial(n): 8: fact = factorial(n) 9: digits = [int(x) for x in str(fact)] 10: return sum(digits)
The factorial() function is defined in a pretty straightforward recursive algorithm. The interesting line stuff happens in the sum_factorial() function (specifically on line 9). We use a list comprehension to unpack the digits in the factorial number into a list object. When the comprehension is evaluated, the call to str() converts the factorial number to a string (which is iterable). We take each character in the string and call int() on it to convert it to an integer. The collection of integers is then collected into a list. the call to sum() on line 10 takes a list of integers and returns a single number which is the sum.